容斥原理与 莫比乌斯 函数

容斥原理

$\left | \bigcup_{i = 1}^{n} \right | = \sum_ {i = 1}^{n} \left |S_i \right | -\sum_{1 \le i < j \le n}^{n} \left |S_i\bigcap S_j \right | +\sum_{1 \le i < j < k \le n} \left | S_i \bigcap S_j \bigcap S_k \right | + ......+ (-1)^{n+1} \left | S_1 \bigcap ...\bigcap S_n \right|$

所以看着是不是非常的头痛，所以我们数形结合用文氏图来直观的表示一下：

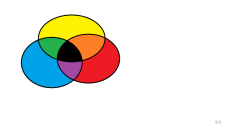
这样就相对直观一点。

接下来我们再看一下 多重集的组合：

设 $S = \left \{ n_1 \cdot a_1,n_2 \cdot a_2,...,n_k \cdot a_k \right \}$ 是由 $n_1$ 个 $a_1$ ，$n_2$ 个 $a_2$ , ..., $n_k$ 个 $a_k$ 组成的多重集。设 $n = \sum_{i = 1}^{k} n_i$ ,对于任意整数 $r \le n$，从 $S$ 中取出 $r$ 个元素组成一个多重集（不考虑顺序），产生的多重集的数量为： $C_{k+r-1}^{k-1}-\sum_{i=1}^{k}C_{k+r-n_i-n_j-3}^{k-1}-...+(-1)^k C_{k+r- \sum_{i=1}^{k}n_i-(k+1)}^{k-1}$

$M \ddot{o}bius$ 函数

设正整数 $N$ 按照算数基本定理分解质因数为 $N=p_{1}^{c_1}p_{2}^{c_2}...p_{m}^{c_m}$， 定义函数
$\mu(N)=\left\{\begin{matrix} 0 & \exists i\in [1,m],c_i>1\\ 1 & m\equiv 0(mod\ 2),\forall i \in[1,m],c_i=1\\ -1 & m\equiv 1 (mod\ 2),\forall i\in [1,m],c_i=1 \end{matrix}\right.$
称 $\mu(N)$ 为 $M \ddot{o}bius$ 函数。

性质

莫比乌斯函数不仅是积性函数，还有如下性质：

$\sum_{d \mid n} \mu(d) = \begin{cases}1&n= 1\\ 0 & n\neq 1\\ \end{cases}$

即 $\sum_{d \mid n}\mu(d) = \varepsilon(n), \mu * 1 = \varepsilon$

证明

设 $n = \displaystyle\prod_{i = 1}^k{p_i}^{c_i}, n' = \prod_{i = 1} ^k p_i$

那么 $\displaystyle\sum_{d \mid n}\mu(d) = \sum_{d \mid n'} = \sum_{i = 0}^k C_k^i\cdot(-1) ^ i = (1 + (-1))^k$

根据二项式定理，易知该式子的值在 $k = 1$ 即 $n = 1$ 是值为 $1$ 否则为 $0$ ， 这也同时证明了 $\displaystyle\sum_{d \mid n}\mu(d) = \left[ n = 1\right] = \varepsilon(n)$ 以及 $\mu * 1 = \varepsilon$

例题

Acwing215 Zap